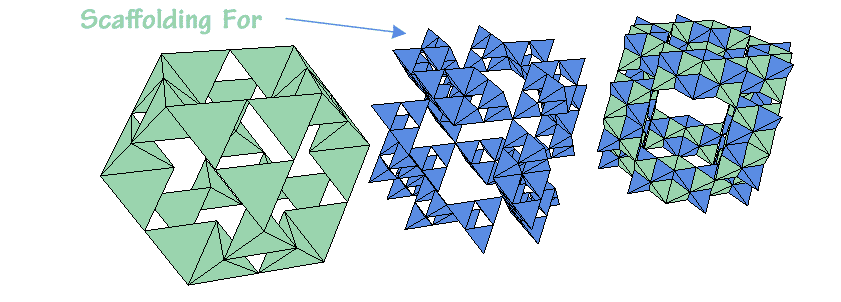
Trihedral Particle Concepts
Even a vague hint long inspired me, that all matter might resonate and like an electronically power-up perpetually like a loaded circuit, or something like ubiquitous electrification, where all particles of matter are perpetually charged by a common source, (for a universe duration). This idea continued a search for knowledge, despite that such hypotheses are absent from popular science. Fundamental particle principles and a developing concept was modeled for contemplation and for possible, continued relevance.
At its first posting in 2020, this webpage had attempted to correspond with a theory closer to the standard model of physics, and that motivation soon expired. Years later with its content reorganized and expanded, some original geometric models remain as independent rationalizations, still as a concentric waveform and as a fundamental 3D particle-structure, which resonates and keeps intact, tetra-directionally and which is sustained by external concentric waves of yet undiscovered, finer densities, of matter-in-motion.
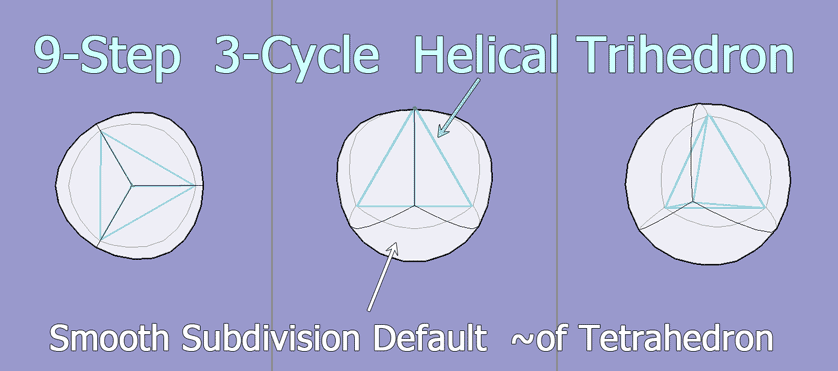
The trihedral (greenish-blue) form above, represents a nine step, multi-axial helix, (with four converging tetrahedral poles not shown), and the white bulging quadrants represent a sphere, (as a default, generic, smooth object product, and these are products from a pro 3D CAD app).The bulges diverge through each of the upper tetrahedral faces or divisions, which match the circuited dynamics of special flow structure. Multiple terms, concepts and visual forms are synonymously used, to sort out its distinctive aspects. Trihedral, tetrahedral, polyhedral, spherical, helical, here are related in modeling, (in order to contextualize the hypothesized wave mechanics). Common 3D model formats are provided below, for the adjustable trihedral structure as a geometrical model, for 3D software.
Fundamental Structural Concept
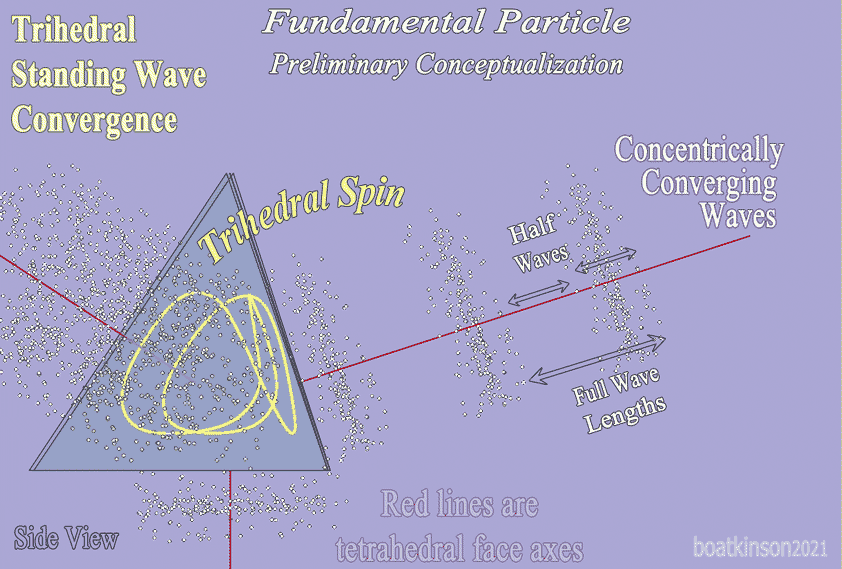
The displayed trihedral form is analogized as a schematic of a universally fundamental particle, the intrinsic geometric convergence of which is tested as a basis of "concentric wave solidification", resulting from four pole, tetrahedral vorticity, (of a trihedral helix). Applicability of this resultant form, is tested as the three dimensional structuration of matter. A variety of geometric variations are together analogized, while leaving the ever finer determinations of parameter distinctions for separate consideration.
Above: Two wave fronts both converging on the left occlude each other's wave front distinctions. Presently it is structural geometry under consideration, offered for testing of it's qualities.
Below: A lower resolution of parameters are shown to convey the triaxial vortex. In the formZ geometry app, there is provided, a generic, helix tool set which enabled this discovery, with its spin directionality, governed by optional clockwise versus counter clockwise windings, (which are expected to generate positive or negative polarity); and in addition, the facetted helix form is optionally smoothed-out in various, optional axial directions, by a separate curve tool. .
Geometrically speaking, white and black figures share the original input source, and were formulated with optional control factors, (where the software can regenerates in a wide range of optional settings, via manual inputs). The white is a smoothed out curve, converted (by a separate tool) from the black-segmented object which consists of just nine straight segments. The white curve is a smoothly converted copy of the black. The lower segmentation in the black wire represents control points for developing smooth curvature (such as the white object). Control points are the standardized, manual-shaping handles for shaping curves, (provided inside geometry software apps).
It is not as yet known whether this software tool produces significant ratios to investigate in nature. Regardless of whether this helix amounts to a programing anomaly or not, in real physical life, the resulting form is verifiable, and the curiously uneven, segment-lengths are yet another matter for study, while this webpage considers both the uniform and our default-nonuniform, segment-lengths, as a valid transition from 2D to 3D mechanics, (from triangle to trihedron).
The black straight (or facetted) wire helix was formed with two radii of two widely differing sizes, (which is key to this geometric function). The collaboration of these two cooperative radii generates the consequential polyhedral-spherical-helical product, analogized as a remotely powered electrical circuit induced with directional flows; however this presuppose the electrical engineering; and, is here hypothesized to transmute undiscovered energies, to be found as finer materials in motion, finer than those defined in the periodic table of elements; and for this expedient hypothesis, one may suppose that energies are simply finer forms of matter which force or impart motion to larger forms of matter, (and suggestive of etheric matter or equivalent terms).
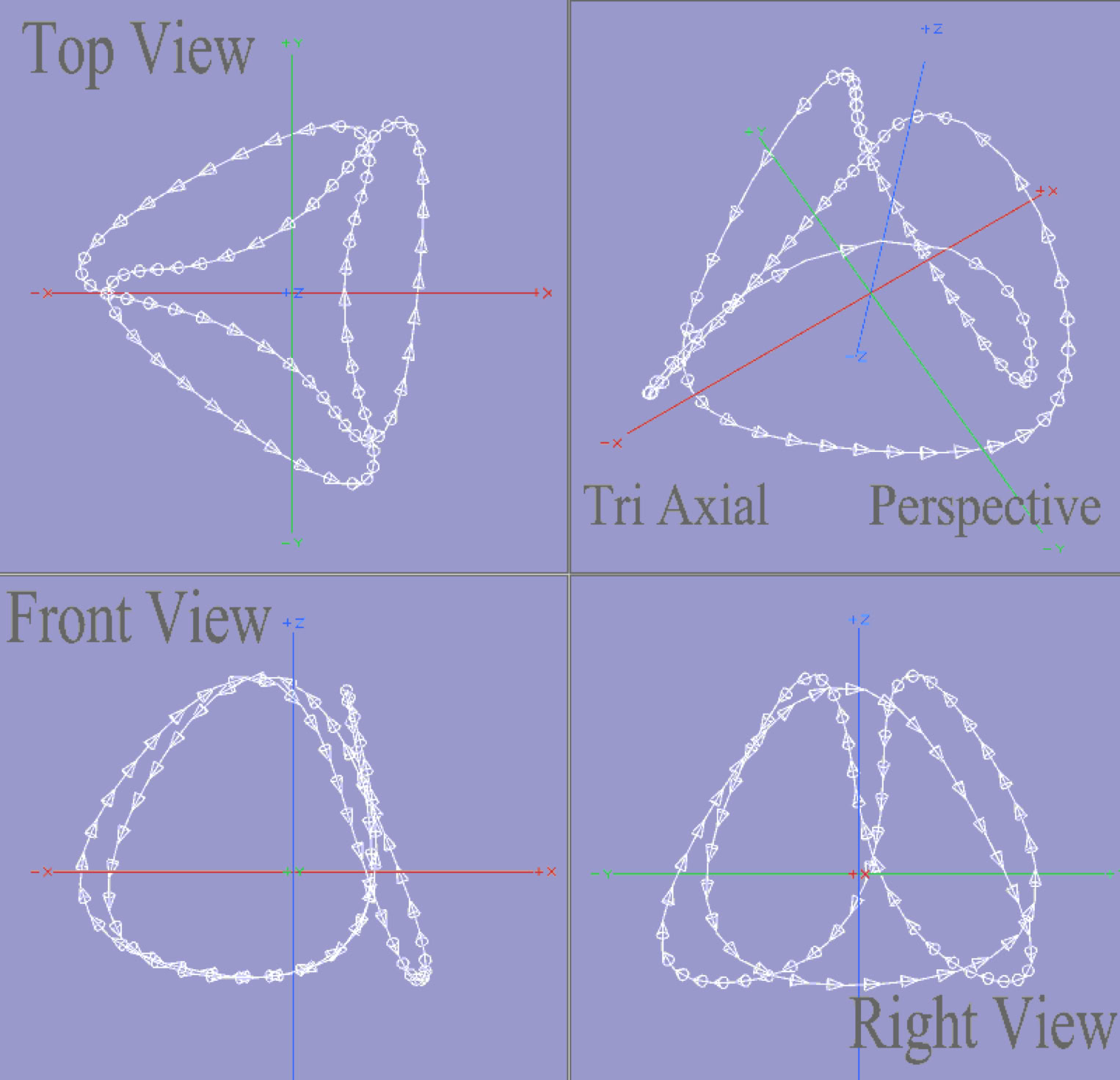
Said otherwise, an orbiting center, instead of a stationary center, unifies a multi-axis-rotary-circuit. Thankfully an older software tool achieves all these steps very efficiently, providing that the software user inputs the stated criteria, in the right order. That which orbits or rotates is taken as the necessary internally flowing configuration, of solid physical matter, and is here symbolized by arrowheads placed along the drawn lines, (and curves), to indicate a perpetuated flow, and by analogy is also hypothesized as the perpetual motion of the universe.
Two Radii And Not One
In contrast to well formed particles, an inadequate ratio of radius size may hypothetically account for short lived particle states, and unstable states of matter. An orbital motion around three consecutive orbital axes, as a closed path, may constitute the initialization, of a trihedral waveform as next proposed.
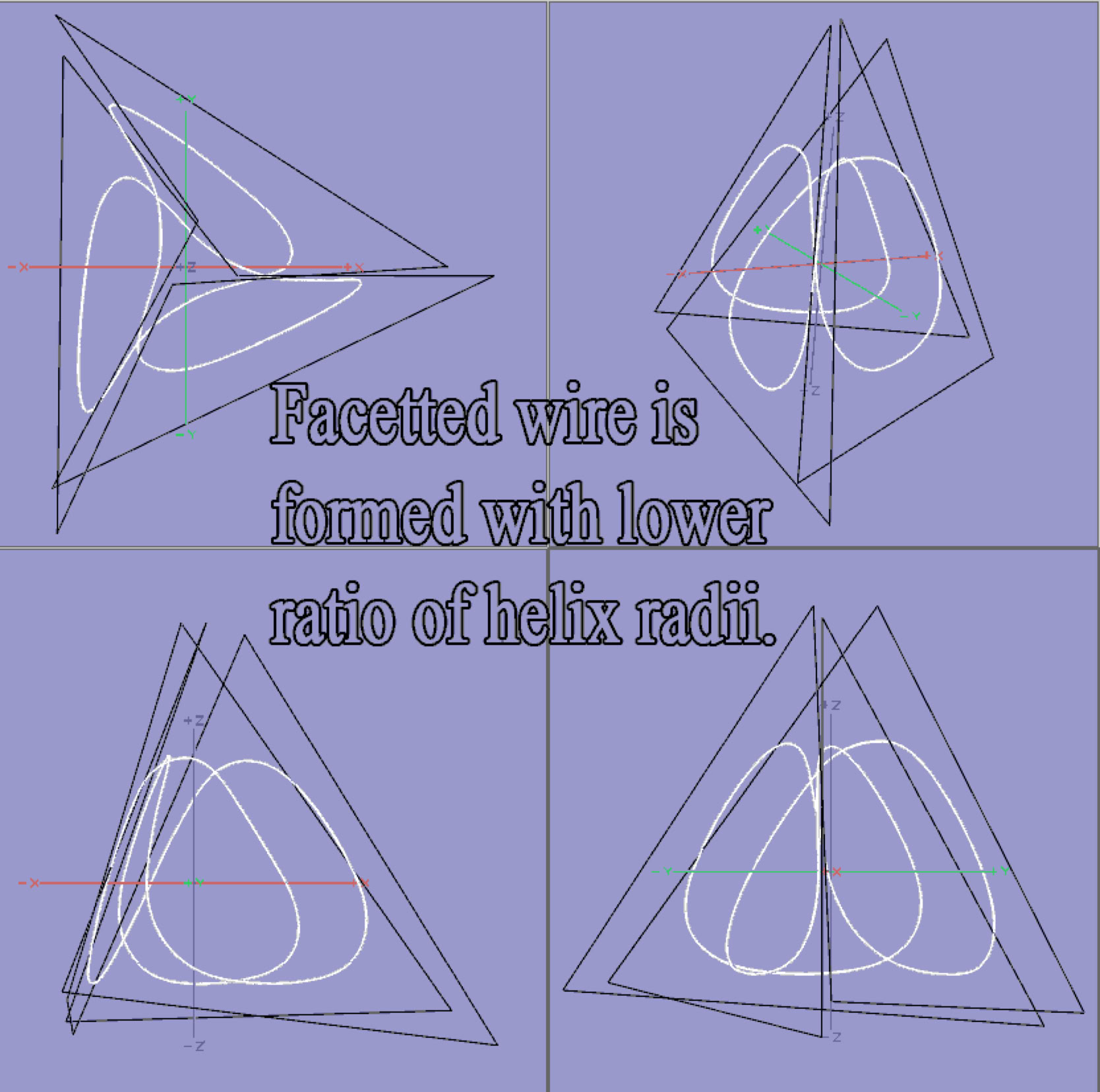
The diagram below shows a facetted helix and its path of winding, both of whose radii are made equal in this diagram, and this ratio of one-to-one, generates a helix around the red equilateral triangle. The fact of two codependent radii instead of one radius is the proposed mechanism to vary particle tightness, both of particle form and also of particle stability. The four diagramed parts, (below), indicate top view on left, perspective view on top right, front view on bottom left and right-side view on bottom right.
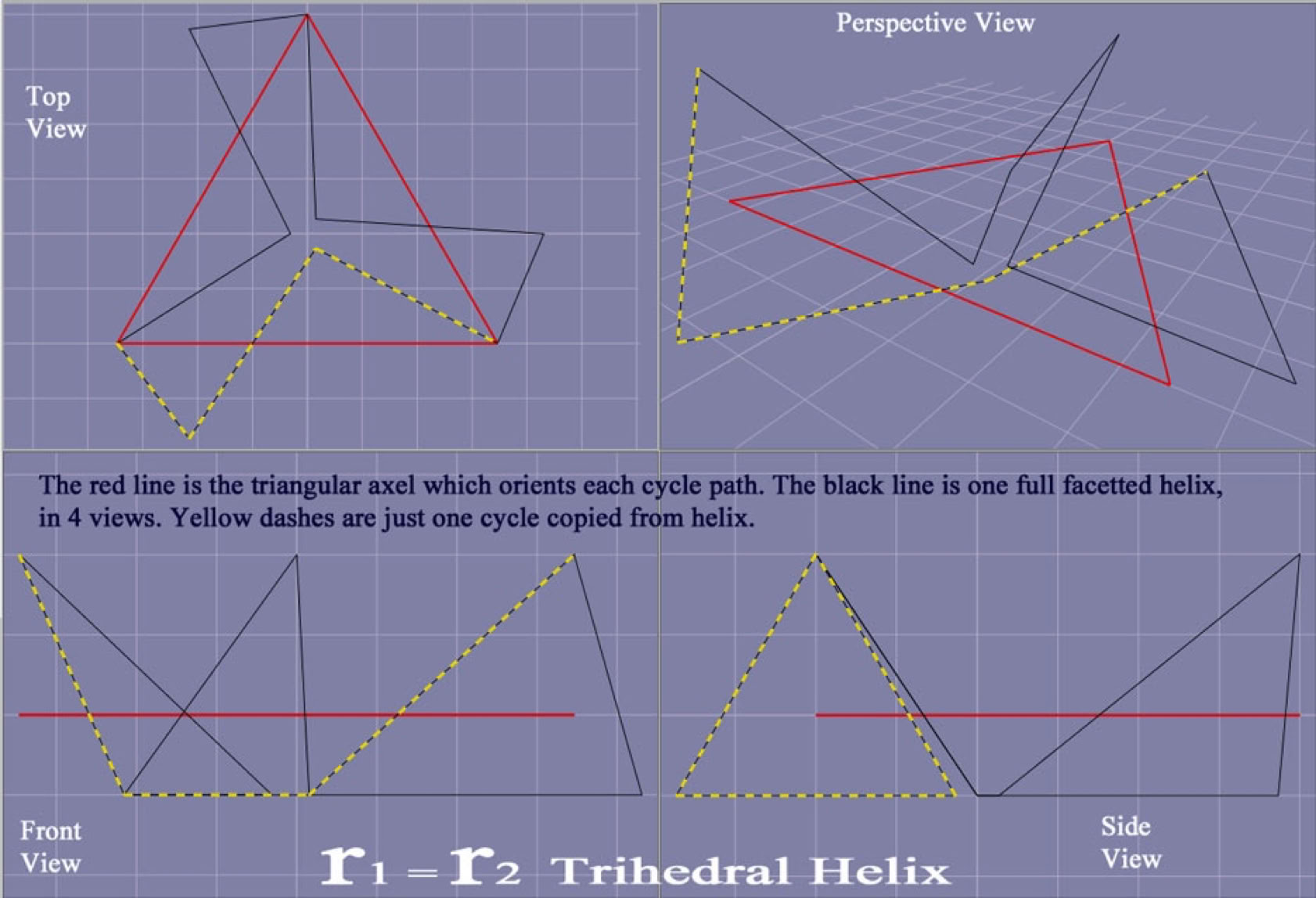
This vectorial diagram above represents the dual orbits, (and optionally as the control points for smooth orbiting curves in earlier images). The primary orbit is an equilateral triangular path in red, while the secondary orbit is the black helix cycling three turns, with nine steps, while the yellow 3D section of the helix indicates just one 3D cycle. Formal geometry defines open and closed wires, segments, surfaces and solids, with potentially useful word applications for particle physics, which are not elaborated in these models.
Below are three displays, one of a close up model to the left, and two zoomed out views to the right of image, as the trihedral helix radius is increased, by sliding (or dragging) the green arrow upwards. The helical radius was enlarged while the vertex gradually converged at the top. The tan color of the trihedral helix signifies the modeling app has the helix under control for increasing helix size, with the green arrow, to slide up or down, centering on on the red-line, (imagined as axel-bearings for radii and indicated by green dots, to left side of image). To the center and right of image: The tan lines or edges of the trihedral-tetra helix have increased much larger, and the red is too tiny to see. By starting close-up (on left of image), the display has to be zoomed way out to progressively see a trihedral tetrahedron (to right of image).
The image below emphasizes the converging vertices to refine polyhedral facets, integrally with helicity.
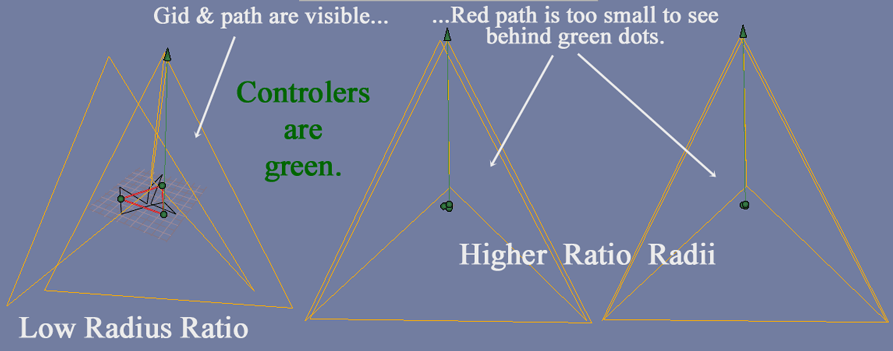
Resilient tightness of edges, might be a necessary rule for the physical property of particle stability. Too small a radius loosens the polyhedral seams. (This refers to the secondary radius mentioned above). The natural rarity of observable short lived particles, may be due in part, to this instability. The smallest ratios of secondary radii, which geometrically form cruder or broken looking enclosures, might well account for the unstable accelerator products as smashed particles, (the so called atomic zoo). Could tight enclosures well describe stable particles?
Specific meanings of trihedra and tetrahedra are both, partly applicable in this hypothesis, because both meanings find applicability in some finer points of this model, and both definitions also overlap proportionally. Trihedra are the simplest enclosures, as defined by fewest parts mathematically, also having a triangulated stability, and furthermore as a helix may form the inherent spin, (which may furthermore offer polarity and force orientation, like electrical charge, through the uncovered base. Next, consider the nature of this as a convergence, with seemingly sealed up trihedral edges, (due to very high ratio of radii, as noted with r1 and r2, along with a much more noticeable "open vertex".

Another note on visual appearance is the 60º projection of a 3 point perspective, above to right, as compared with the close-up, 0º axonometric view to right above, (achieved by zooming in and out of the 3D model). Three sufficiently closed helical loops and one resulting open helical loop, bind together as a self stabilizing, trihedral helix.
The multi-view image below is all axonometric, (equivalent to zero perspective and this explains the flatter look of the angled view).
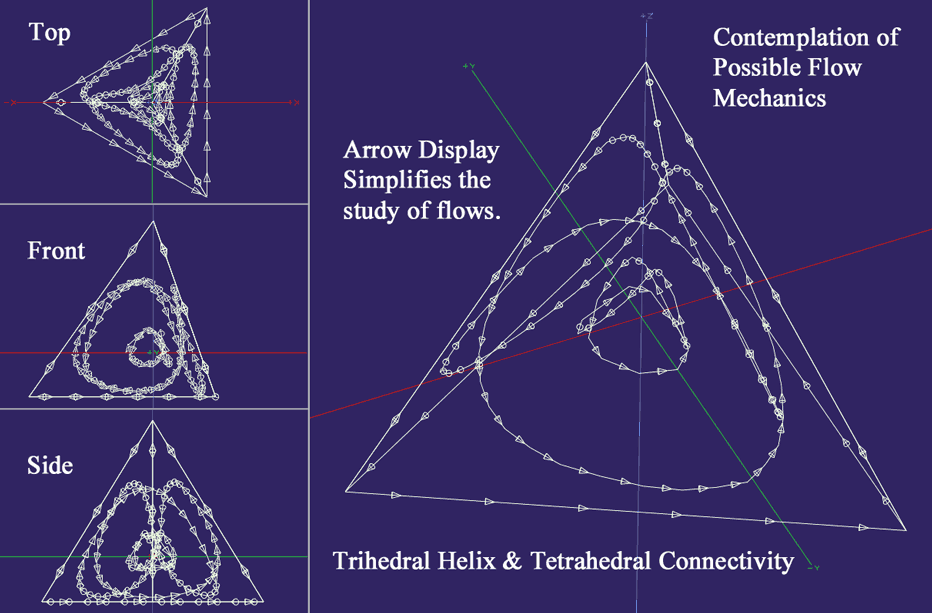
Would two, codependent, orbiting paths clarify particle functionality, as compared with singular pivotal-spins? Rotation and flow are key particulars and other properties were also studied on an earlier webpage, (link).These trihedral models may be tested to explain the most fundamental particles as, a pyramidal framework which branches a polarity in three directions from the base, (one branch through each pyramid face and one root as the base). A 3D geometric stability might satisfactorily describe a 3D universe stability, to be further considered, for higher ratios of r1 and r2, which tighten up the edges.
These geometric frameworks present multiple conceivable connection modalities, which must be rationalized with other scientific facts, before devoting too much time to speculative 3D modeling. If physical evidence demands a tetrahedral form factor, then the trihedron can be manually adjusted to match, and this can be manually modeled without loosing finer features. The parallel edges which are finely separated, provide one infinitesimal crack on each of the three vertical faces, symmetrically angled at 120º from each other, and the exacting ratios of proportions is worth a closer mathematical evaluation, which may assist designing experiments.

A "tiny hole" at the trihedron apex, (orthogonally respective to base), can evade observation, but zooming in closely does reveal it clearly, (as in the image above). It orthogonally projects as the same size to the tiny triangulating-concentric-axel. The image above magnifies the hole with it's signature separation of parallel wires, which become closer at higher ratios of r1 and r2.
Note that the formZ version 9 app forces a 'covering' (as they call it), on to helices, which can be removed with their 'Uncover' tool, and this default covering does obscure the open apex observation when shading of the display is enabled. Unfortunately for the experimenter, this removal of the unwanted covering voids the parametric adjustability of the helix, except and unless an older version of formZ is used, in which case the parameterization of the helix is preserved for experimental editing purposes. Versions 8 and prior versions dating back into the 1900s all benefited from the same helix tool , (not seen in other brands of CAD)..
The basis of this 3D model was discovered long before attempting to detail it's potentials for atomic applicability. Detailing and organizing the loose ends seemed overwhelming, without knowing of any supportive basis, until increasing anologies were considered by the study of Pythagoreanhylozoics.
Would branching polarity trough tetrahedral faces differ from conventionally taught linear polarity? Could multi axial, codependent, orbiting paths clarify particle functionality, as compared with singular pivotal-spins? These trihedral models may be tested to explain the most fundamental particles as, a walled in "surface object", which shapes a branching polarity, which might subsequently govern atomic bonding rules.
Helix Tool Defaults
One definition of good or clean geometry is absence of crossing faces or crossing segments. A non-self-crossing, smooth outcome can otherwise be manually obtained by converting the faceted trihedral helix into a plain object, (free of parameterization), and then converting it to a desirable curve, (as there are multiple kinds of curves to suit a purpose like visualizing the results displayed on this page).
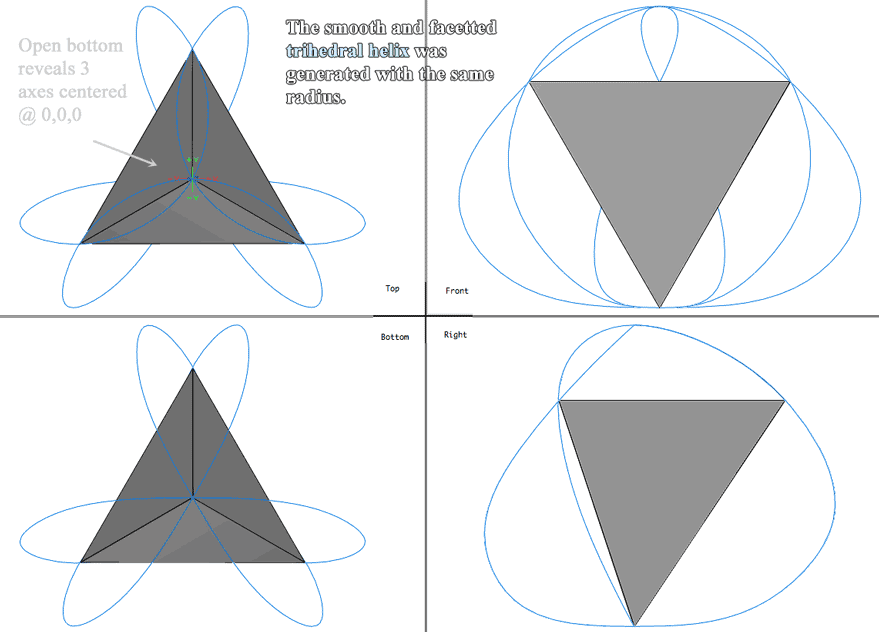
The formZ, built in option of helix parameters offers this instant, optional spherical representation, (blue curve). It appears as a physical wire strung around one common center and four vertices in a polar fashion, which looses the trihedral surface-solid or boundary representation. So that the truer trihedral helix is lost in the rounding off of typical helix-tools, and therefore the curved or smooth representations must instead be manually derived. At some point these parameters may be explored in other apps like Rhinocerus 3D software.
Smooth Versus Facetted
Other parameterized tools, (generally known as smooth geometry for curve and surface editing), were partly explored for helical modeling. The following is a semi-transparent model based on the same 3 cycle, 9 step, faceted-helix. The value of this type of smooth object would be to further explore possibilities of internal-particle-sphericity, omnidirectional, trihedral spin and conceivable properties in 3D space. (The model below is a simple conversion from a facetted version of the helical tetrahedron into a default smooth object. Smooth tools provide for multiple solutions of varied forms, which at this point are less pressing to review. The default crossing faces deserve exploratory editing.
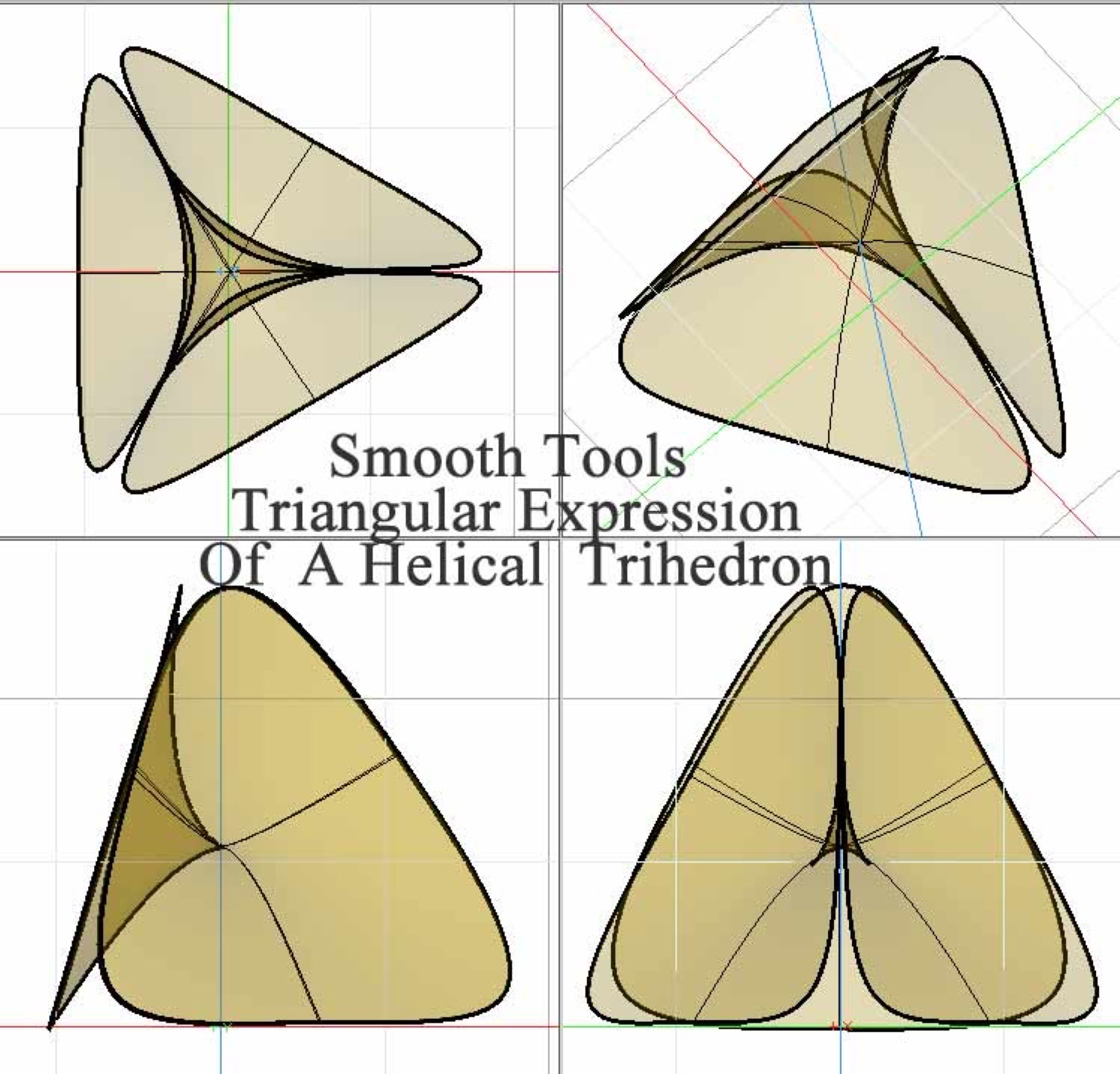
______
In the spirit of collaboration, I invite interested persons to discuss this subject matter, and the modeling approaches, possibly through zoom, or other venues, emailing, etc. is also welcome. Please test the 3D model with your 3D software at your convenience, and let me know if the files need refreshing as this website has lost some data, over it's many years on-line.
Simple Models In Differing 3D Formats
In the spirit of free software uses, here is a quick way to immediately see the arrows intrinsically within a 3D software app. Other, excellent software brands have lacked this particular automated arrow tool, and instead offer other sorts of excellent, automated tools. Verifying this model with other modeling software brands may add some insights. Otherwise for immediate, cost-free viewing of this model, with its arrows intact, the formz free app, 0$ for Windows & Mac is downloaded here.
Automatized arrow checking simplifies a more detailed modeling of directions, polarities and chirality, but the model above is at a simple, preliminary stage. (This display option can be easily toggled, or turned on or off, under formZ/M e n u/Display/Display Options, and at the bottom of the dialog-panel, the "show direction" box can be checked or unchecked, to toggle the display of arrows.) Far greater detail of flows is easier to model in this way, with repeated toggling, to better distinguish hypothetical parts and functions, and to avoid a lot of manual modeling work of modeling the arrows manually. Direction of vorticity is a possible aid to considering atomic architecture.
It is known among 3D modelers that importing and exporting certain 3D formats looses specialized modeling features such as arrows and other things. Only plain conventions like lines, surfaces and solids, have been reliably universalized. Conventions of handling geometry also varies from one app brand to another. and yet access to highly developed software is made free, to preview the full potentials.
Plain 100:1 Ratio Trihedral Helix are available:
Facetted trihedral helix with internally facet-rounded, trihedral helices, (but possibly, only formZ will automatically display the arrows as an option already built into formZ). This option can be turned on or off under formZ/Options/Display Options.
The formZ apps natively display flow like arrows:
In recent years formZ added a default auto-surfacing feature to its helix tool, and if the surface component is removed from the helix, then the helix -parameters are lost. Adjustable parameters allow the observer to study the effects of vast ratio-zooming, to contemplate the effects of a nano radius upon the macro world. This may call for keeping copies of the parameterized helix along with the naked wire helix, which is more work than the older formZ version. Yet the surfacing feature is otherwise useful to simulate the helix as a converging surface solid,.
Next described are the attempts to model the tetrahedral surface division. This conformsto preceding trihedral and tetrahedral modeling to correspond workings of a spherical standing wave.
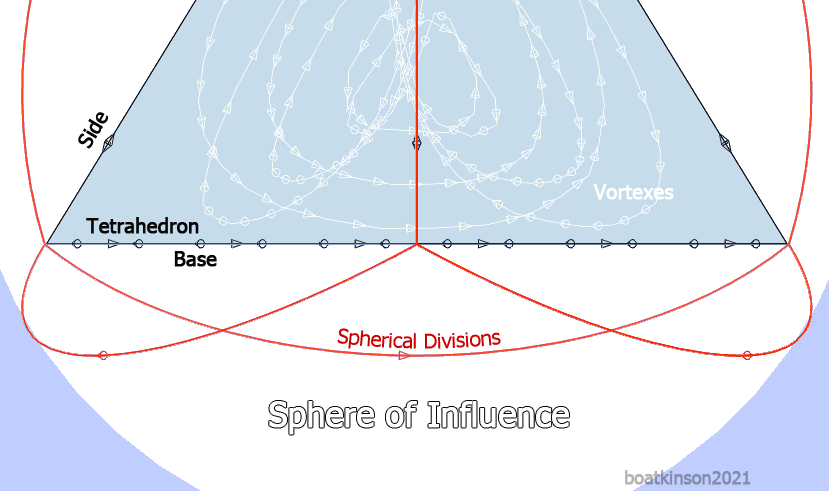
Spheres of Influence
Resonant, spherical waves are questioned as fundamental particles, or building components of organized matter. Interspace between spheres is posed as a conduit of the common resonation. Comparative or interchangeable versions of smooth and facetted geometry avoid a premature specialization of form or sphericity. A "branching polarity" may deserve a more particularized spherosity rather than the traditional polar mapping of spheres, because the innards are hypothesized as multi axial and rotatory, and this differs from a spinning ball analogy, orbiting around a sun.
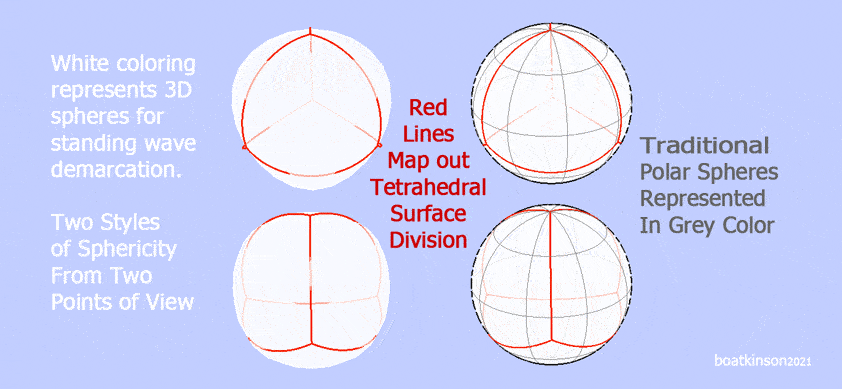
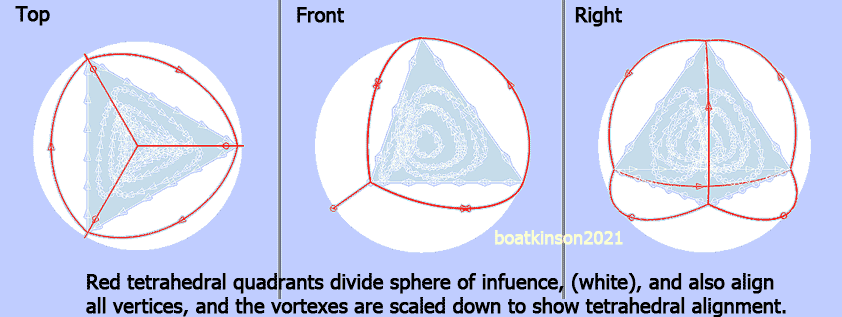
Tetrahedral quadrants divide and define a sphere of influence, and also align with tetrahedral vertices. The three vortex axes branch one pole each, while the converged base axis is of opposite polarity. Rotary directionality is a key property of physical, organized matter, and the trihedral spacing between parallel, neighboring edges does insulate the opposing flow directions, while the base of the trihedron bears just one direction of flow which internally branches through the upper three (as a multiaxial split polarity).
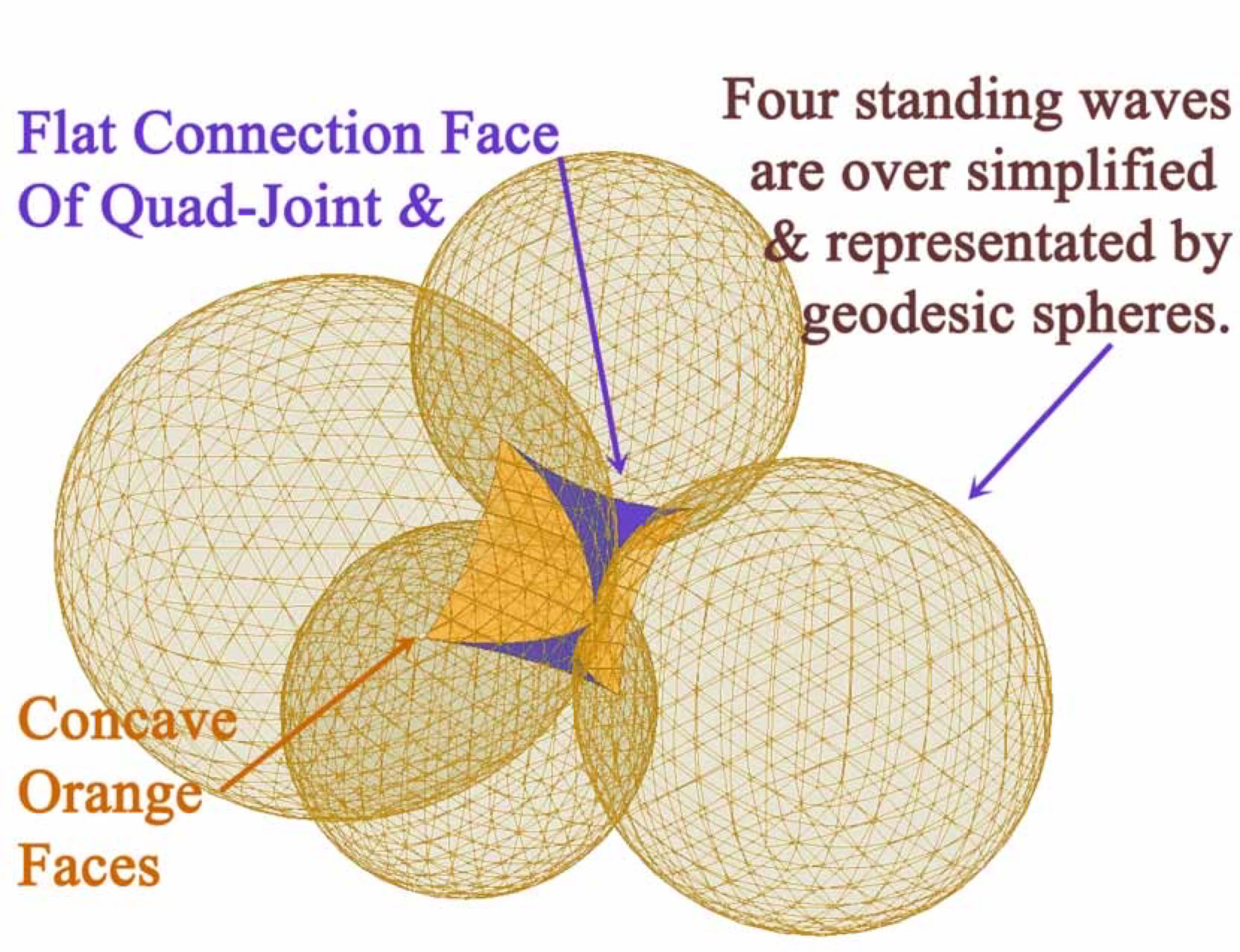
Spheres And Interspaces
Interspaces of geodesic spheres may suggest incompatible cohesion. Only further below will bonding of spheres be briefly touched upon, as mechanics for aggregation of concentric wave particles might require specific a packing mechanism. Ordinary packing of spheres maybe found to lack the tightness found in trihedral packing.

The model of geodesic sphere packing, (above), examines less compaction and greater interspacing of touching spheres. Continuous stacking may not aggregate with concentric wave resonation for the most elementary building blocks for matter. Concentrically omnidirectional wave pressurization may permeate the roomy interspaces of so called :cnnon ball packing” configurations of spheres.
Next, just four spheres are modeled to observe the form of the resulting interspace
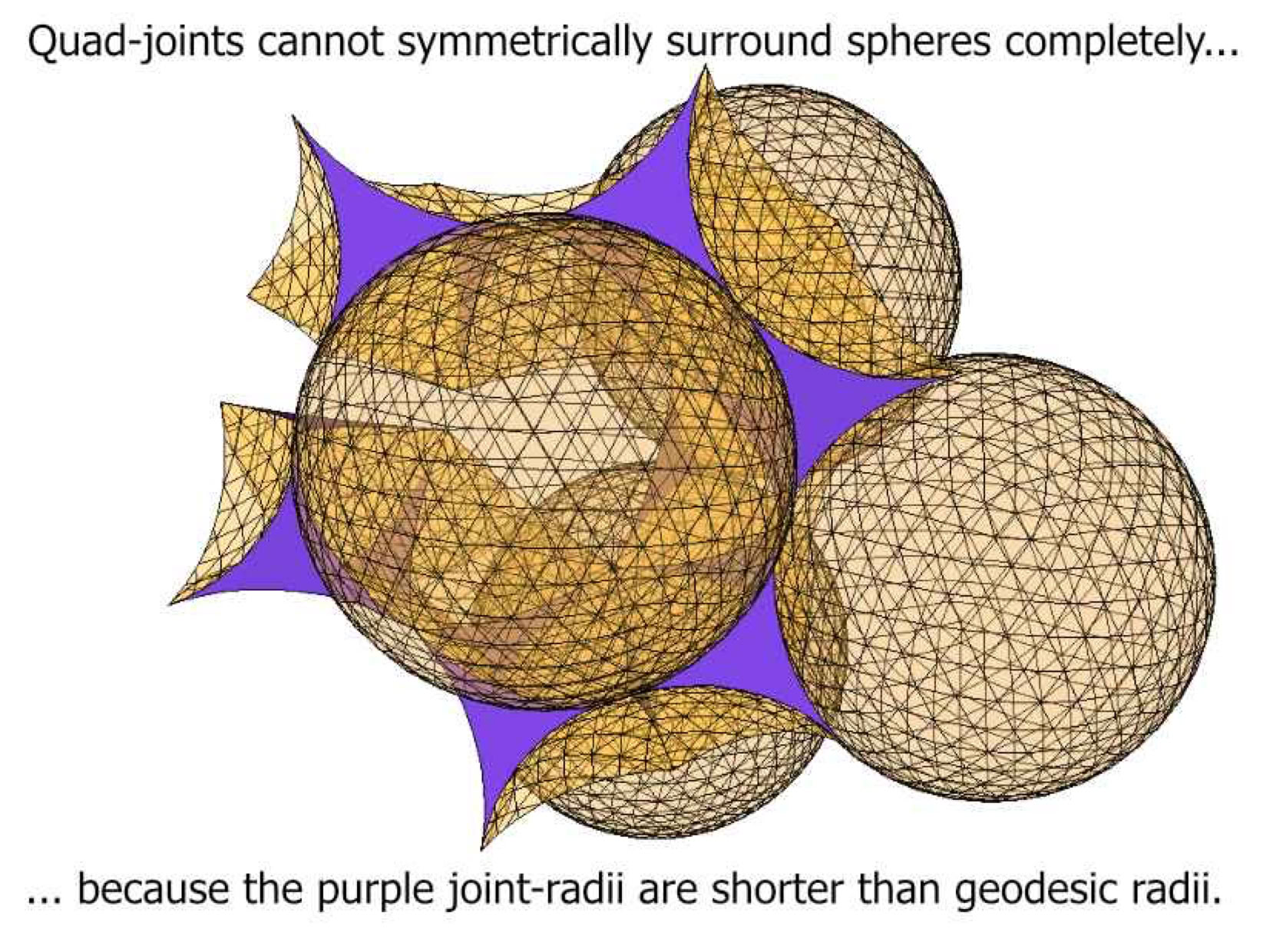
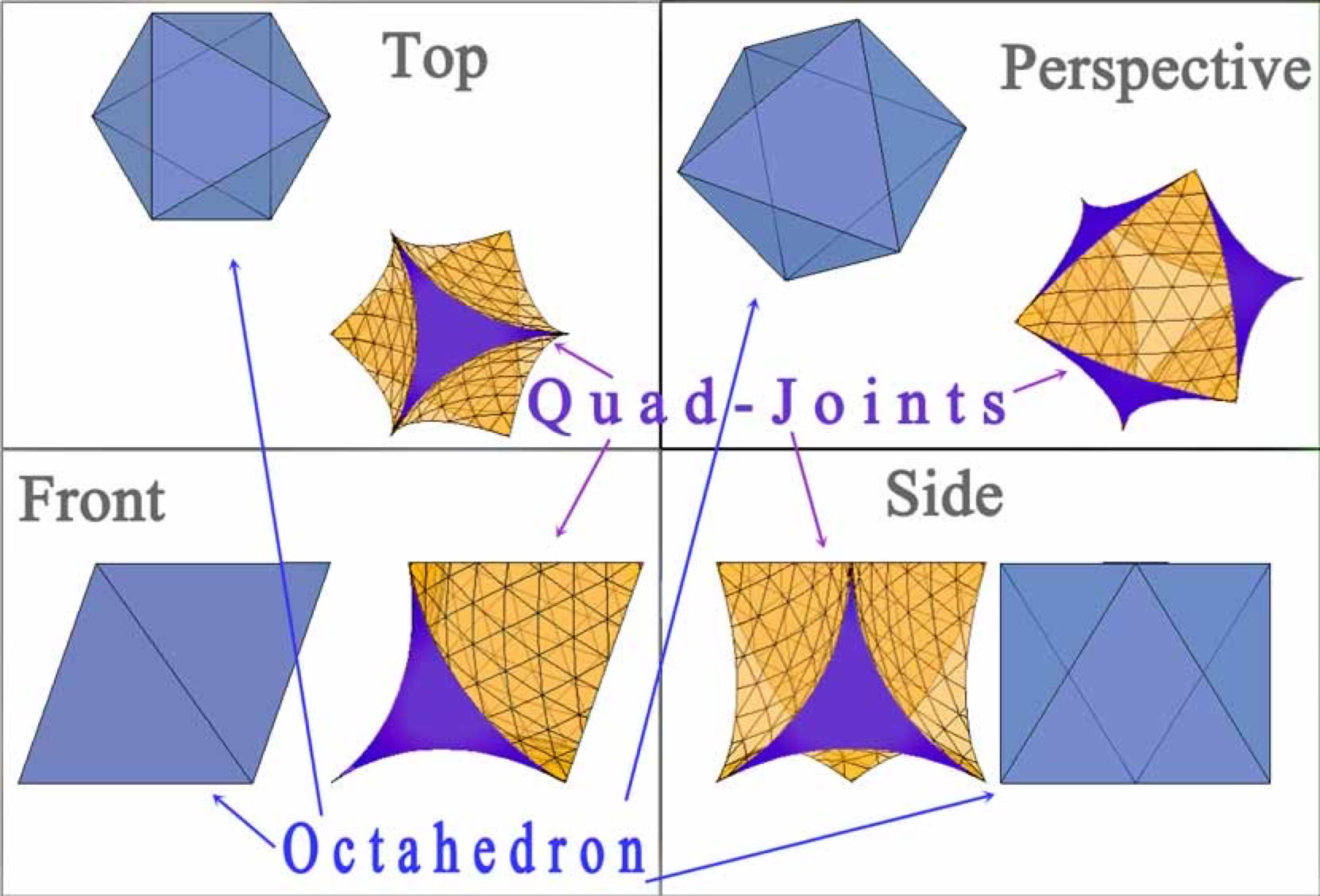
Could minimized space between four identical spheres (which mutually touch) account for cohesion or amalgamation? Possibly due to less inter sphere porosity?
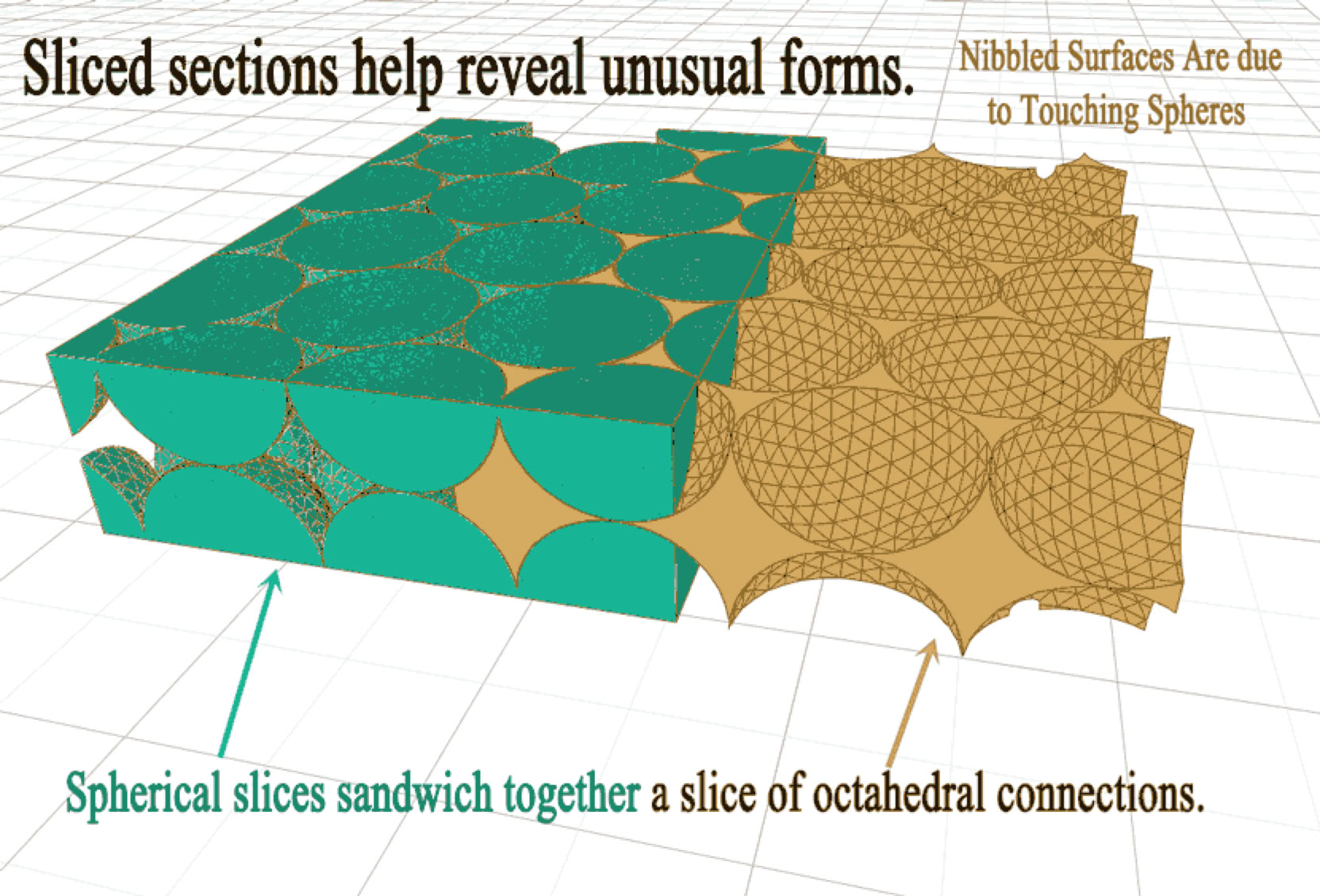
The next model below represents rows and stacked spheres, all sliced to show another version of Interspaces The (green) object on the left is used to boolean-difference the (tan) model on the right, the differenced result of which reveals a non-linear, networked space. This version of networked interspace is just one example of many possible networked or porous interspaces.
Purely geometrical studies of sphere packing are separately published by other people on the www, which might suggest a variety of conceivable, spherical arrangements, which are beyond the scope of the present hypothetical geometrical-layout of concentric waves and Interspaces.
The Motivation to write this out.
Originally, a prize was offered by a sponsor, but this effort could not be completed before the deadline. I decided to post the content to motivate a self dialog, still in need of more work. Much later in 2026 a difficult rewriting of this entire website with better coding was added along with this content, including much in its original, unfinished form.
Preliminary Bonding Concepts
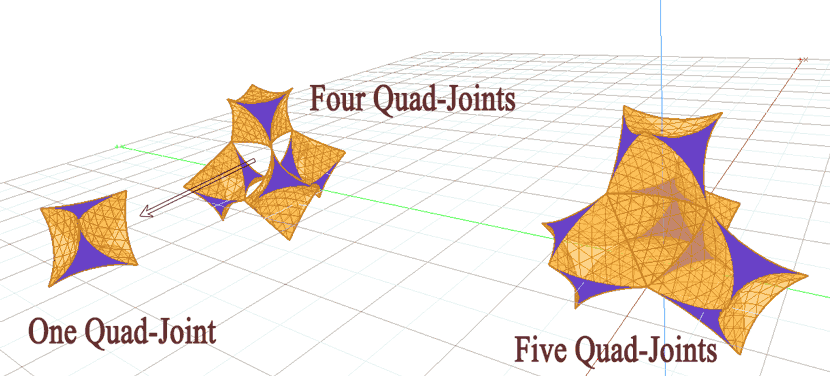
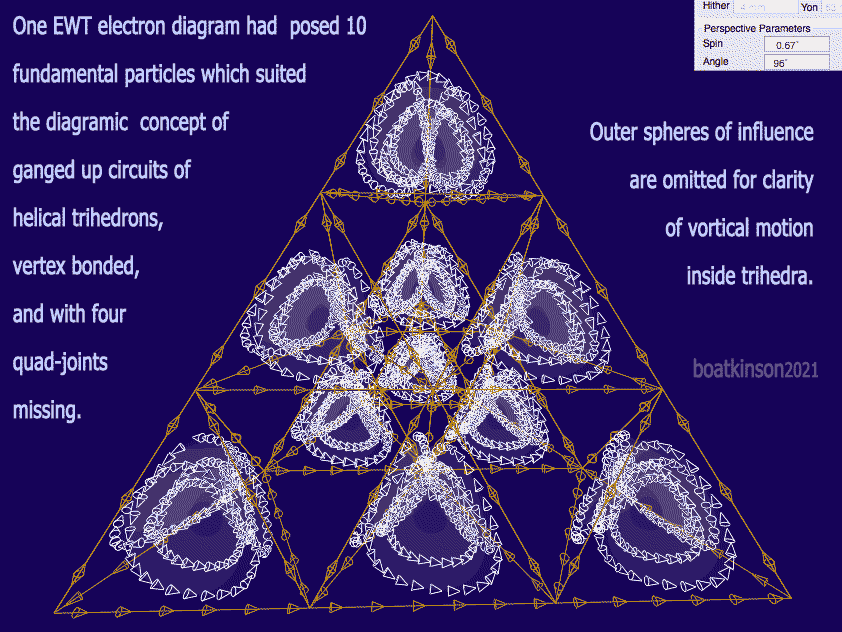
The following trihedral innards of spherical waves were included in the original presentation, and lacked sufficient modeling and work on the surrounding fractal sphericity accruing to compose atomic structures. Could multiple frameworks bond symmetrically at the vertices and or faces? Might such connections train arrows like gears-trains to achieve bonding of larger, aggregate structures?
More modeling is needed to update images, to illustrate update text.
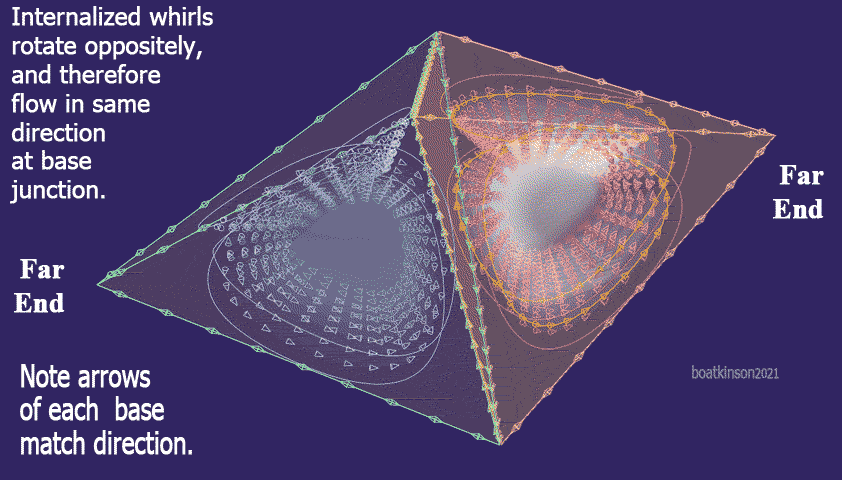
Could positive and negative polarities of particles imply specific directions of rotation? Next, the red and blue coloring indicates that the same trihedral frameworks simply have the arrow directions reversed, and therefor the base arrows are pointing in the same direction. Arrow directions can otherwise imaginatively be drawn together with reversed arrow directions at the trihedral base, to analyze all possible mechanics of base bonding.
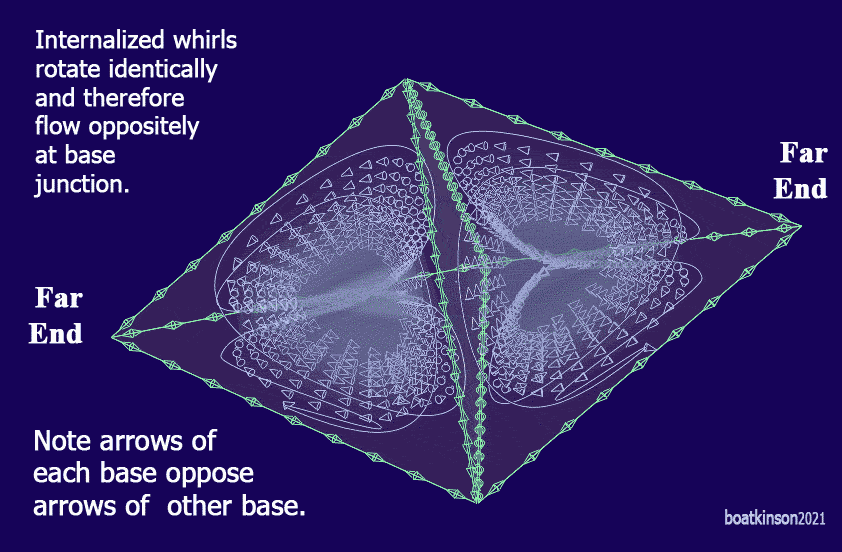
Could reversed arrows shaped like two typed character, <> , signify stability, similar to geometry's rules of well formed objects? Geometry offers multiple modes of assembly to consider and compare the micro and the macro systems. The intent behind images above and below only indicates that variable alignment and chirality factors can be graphically modeled together for analysis of possible mechanics and as an exploration for natural laws.
Could perpetually whirling and concentric waves comprise the fundamental particle of organized matter? Could this helical trihedron be maintained (or powered), by external, symmetrical vibrations, in concert with neighboring particles in the universe? Could these forceful vibrations operate in the interspace domains described earlier?
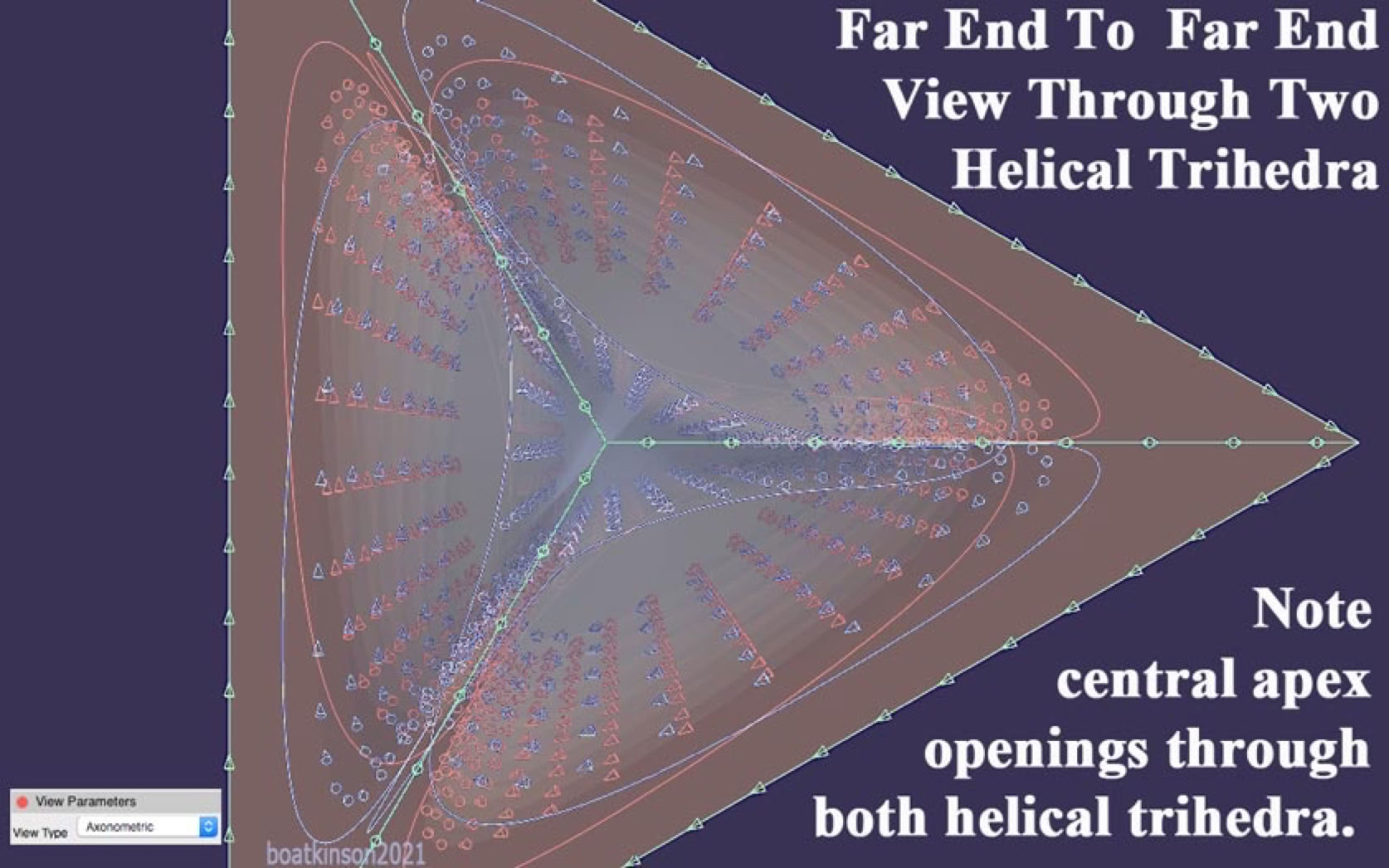
Next, examples of bonding at vertices are modeled with symmetrical alignments. The finer details of arrow and circuit analogies are not further explored here, and are rather left as open examples of possibilities that fit mechanical analogies

The focussed on classical equations and constants to determine geometric relationships, whereas this webpage is only exploring several polyhedral structures. This star tetrahedron model omits the central tetrahedral vortices, (graphically speaking), which poses further open questions about the differential properties, of "thorough solidity" as in classical tetrahedrons versus "surface solidity" (of trihedrons), and both concepts raise open questions.
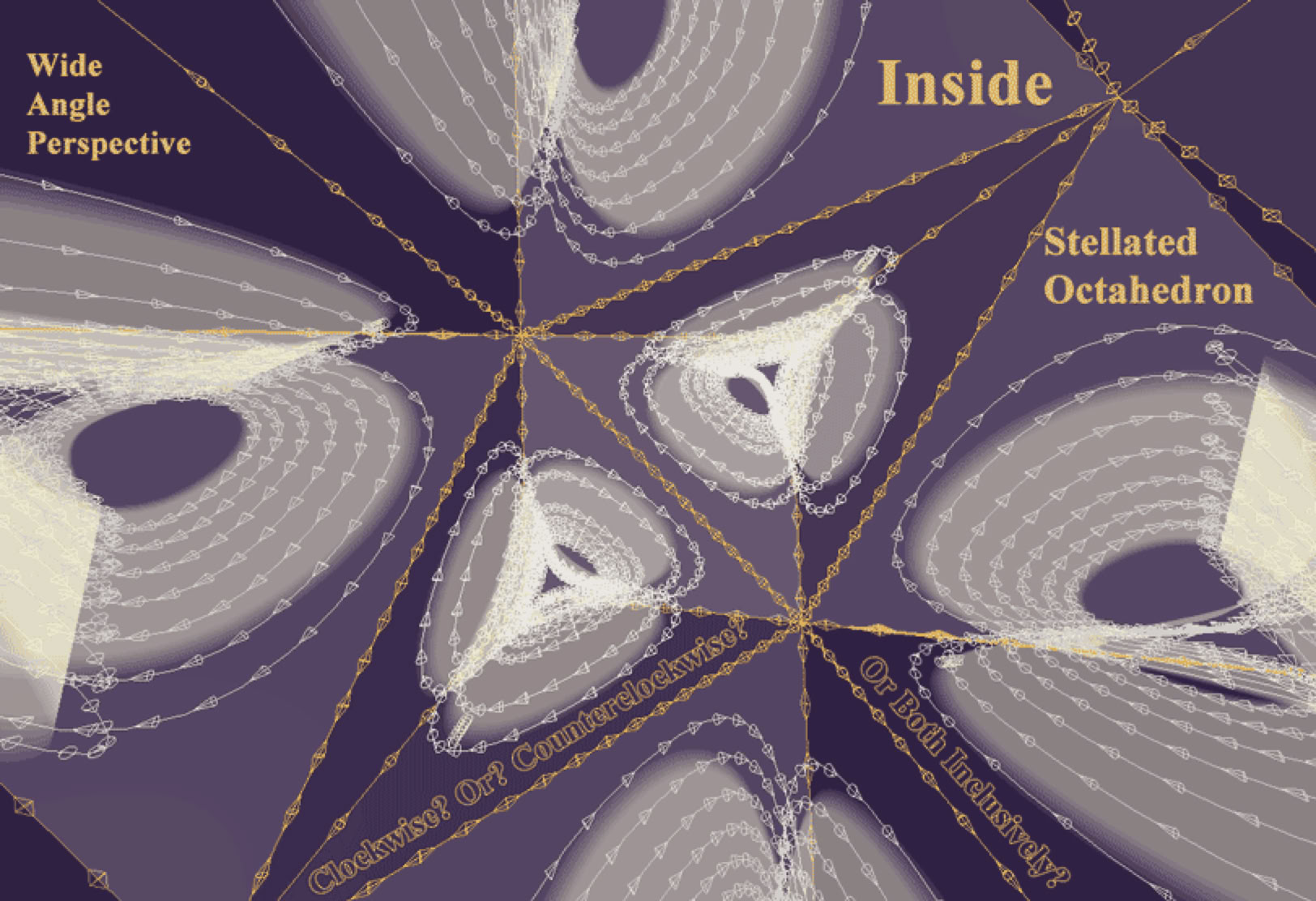
"The stellated octahedron is the only stellation of the octahedron. It was depicted by Leonardo da Vinci in Pacioli's book 'De Divina Proportione' in 1509. A hundred years later was named 'Stella octangula' by Johannes Kepler."
I quickly adopted computer modeling specifically when the 3D modeling first became affordable, around the mid 1990s, when I found the formZ app which included platonic solids modeling, smooth formed NURBS modeling, curves, spirals, colorful rendering, text and printing, along with good educational support, all in one package without any need of specialized programming skills. This combination suited many expedient needs. Many other kinds of inspirations of life, along with idealized forms of geometry are milestones of evolution, planted in higher dimensions to pour downward as energies into our lower three dimensional world, which can naturally motivate lower beings, to grow forwardly in knowledge, and thrust our way through and beyond the densest, condensed matter.
The 3D software apps are becoming easier to use and to model concepts of 3D material structure. Earlier work exploring methods.